Um pouco da história dos números
Hoje podemos responder à pergunta anterior com facilidade, mas nem sempre foi assim. A humanidade levou centenas de milhares de anos para construir a ideia de número. É isso mesmo! Antigamente, a Matemática não existia na forma que conhecemos hoje.
Sistemas de Numeração
Na maior parte da história da humanidade, as pessoas não sabiam contar! E como elas aprenderam? Provavelmente a partir de suas necessidades práticas. Quando as antigas civilizações começaram a criar animais e plantar, contar passou a ser importante para que pudessem controlar o que possuíam.
Aprendendo a contar
Veja uma situação que pode ter acontecido em um tempo bem distante. De manhã, a pastora separava uma pedrinha para cada ovelha que levava para pastar. Essas pedrinhas eram guardadas em um saquinho. À tarde, a pastora comparava a quantidade de ovelhas que voltava do pasto com a quantidade de pedrinhas do saquinho. Se não sobrassem pedrinhas após a passagem do rebanho, ela sabia que todas as ovelhas haviam voltado.
Vamos pensar um pouco!!!!!
Em certa classe, o número de carteiras é igual ao número de alunos. Um dia, ao chegar na sala, o professor observou duas carteiras vazias e comentou que dois alunos haviam faltado. O comentário dele tem relação com o processo de contagem usado pela pastora dos quadrinhos? Justifiquem sua resposta.
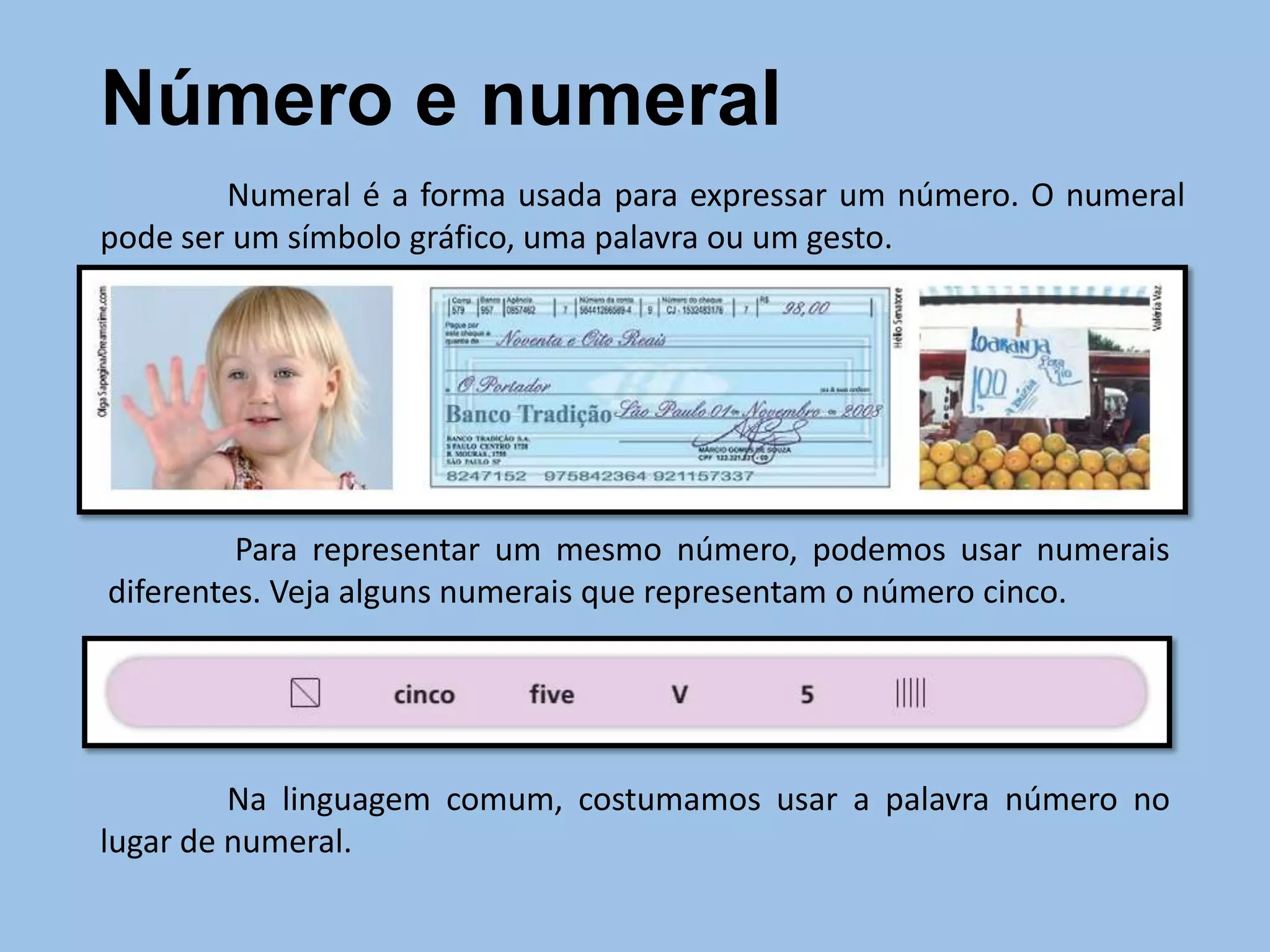
Número e numeral
Numeral é a forma usada para expressar um número.
O numeral pode ser um símbolo gráfico, uma palavra ou um gesto. Para representar um mesmo número, podemos usar numerais diferentes. Veja alguns numerais que representam o número cinco.
Na linguagem comum, costumamos usar a palavra número no lugar de numeral.
1. Observe as ilustrações e responda.
a) Em qual situação há menos jogadores do que bolas?
b) Em qual situação há mais jogadores do que bolas?
c) Em qual situação os jogadores são tantos quantas são as bolas?
d) Para responder a essas perguntas precisa saber contar?
2. A quantidade de latas de refrigerante consumidas durante uma festa, num restaurante, foi registrada de dois modos: Em qual dessas anotações é mais fácil ler o resultado? Por quê?
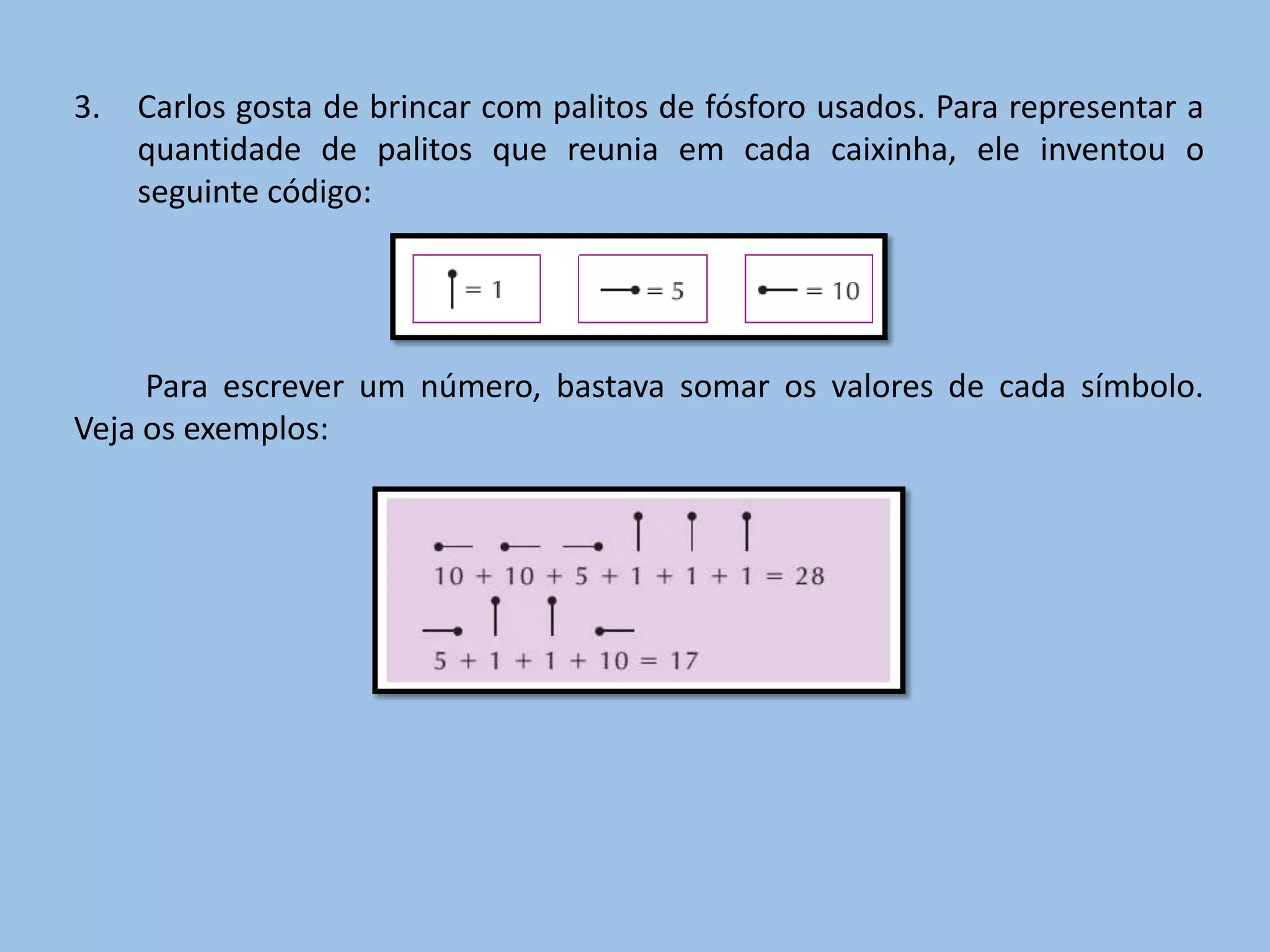
3. Carlos gosta de brincar com palitos de fósforo usados. Para representar a quantidade de palitos que reunia em cada caixinha, ele inventou o seguinte código: Para escrever um número, bastava somar os valores de cada símbolo. Veja os exemplos:
Agora é a sua vez!
Escreva em seu caderno o número representado em cada situação.
Criando símbolos e regras
Outra dificuldade que as pessoas provavelmente encontravam, há milhares de anos, era trabalhar com grandes quantidades. Afinal, registrar essas quantidades empilhando pedras ou fazendo marcas na madeira era difícil e pouco prático. Daí veio a ideia de agrupar, para visualizar melhor as quantidades, criando símbolos especiais para esses agrupamentos e regras para registrar quantidades com esses símbolos. Surgiam, então, os primeiros sistemas de numeração.
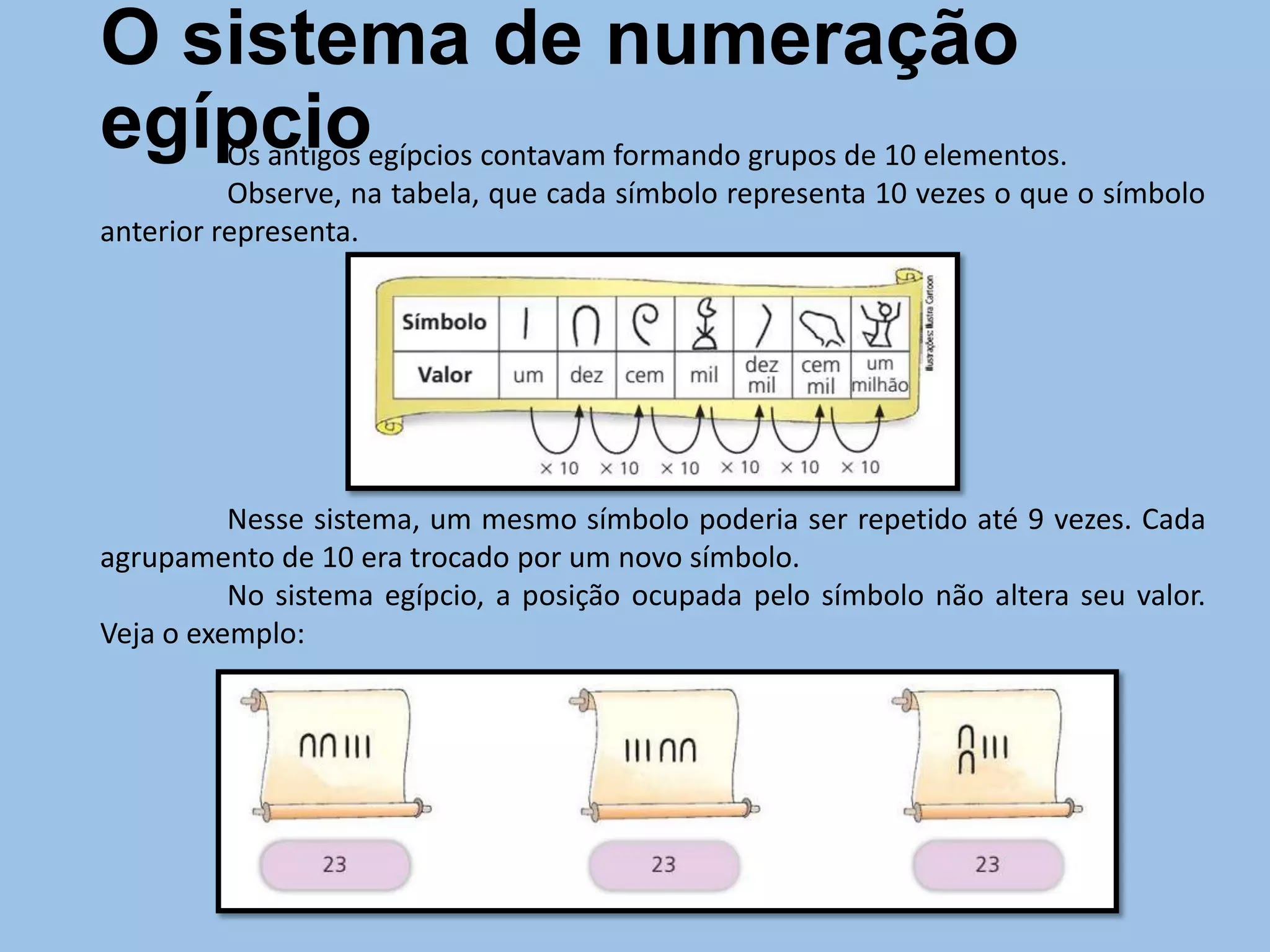
O sistema de numeração egípcio
Os antigos egípcios contavam formando grupos de 10 elementos. Observe, na tabela, que cada símbolo representa 10 vezes o que o símbolo anterior representa. Nesse sistema, um mesmo símbolo poderia ser repetido até 9 vezes. Cada agrupamento de 10 era trocado por um novo símbolo. No sistema egípcio, a posição ocupada pelo símbolo não altera seu valor. Veja o exemplo:
Representação do número 999 no sistema egípcio.
Veja a adição 86 + 47 no sistema egípcio.
O sistema de numeração romano
Os antigos romanos também possuíam um sistema de numeração formado por sete símbolos. Observe os exemplos de números escritos em nosso sistema e no sistema romano.
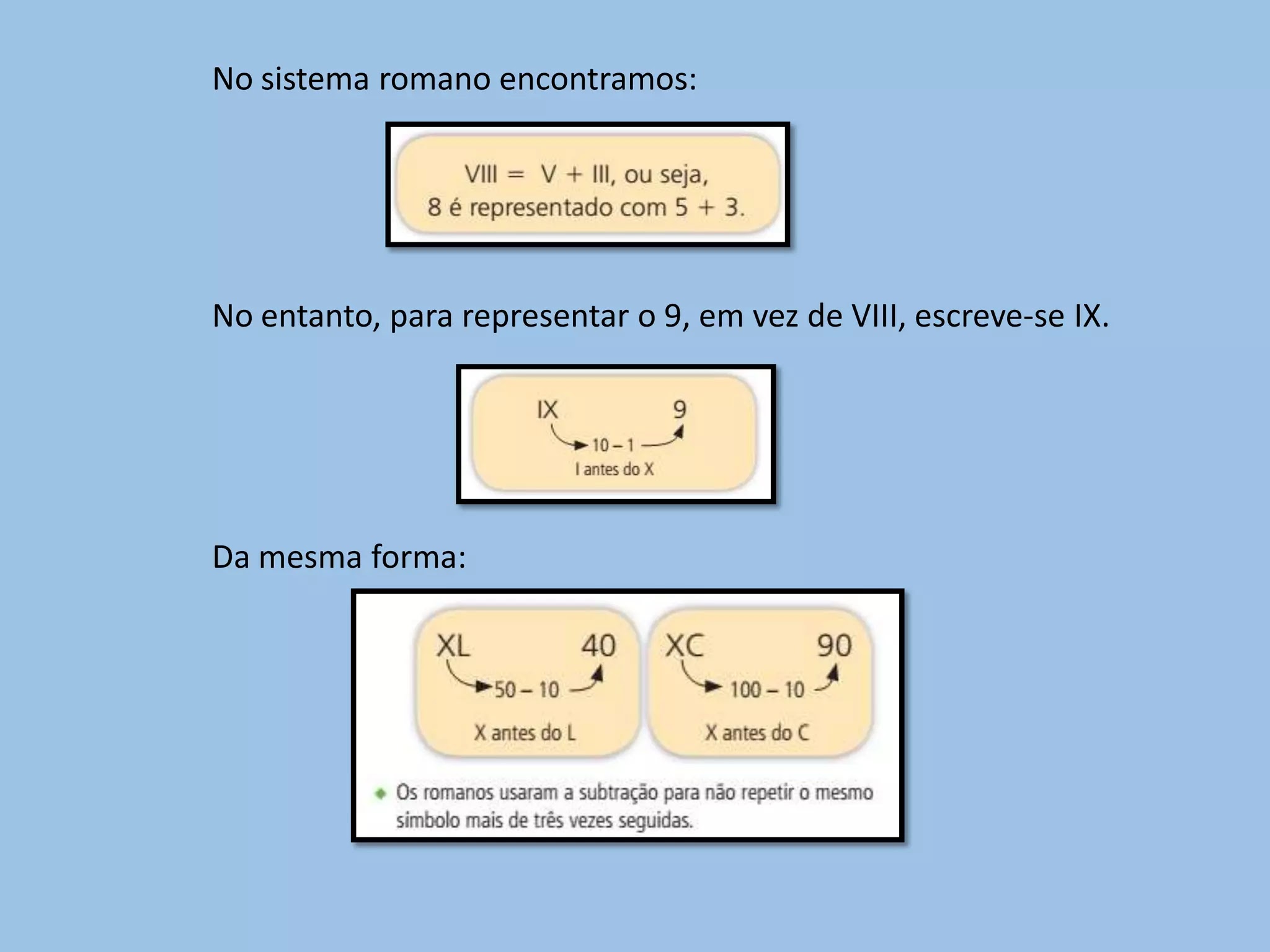
No sistema romano encontramos: No entanto, para representar o 9, em vez de VIII, escreve-se IX. Da mesma forma:
Durante mais de 1000 anos, o sistema de numeração romano foi utilizado na Europa. Por volta do século XIII, com a expansão do comércio e das navegações, os símbolos romanos foram substituídos pelos algarismos indo arábicos. Hoje, a numeração romana ainda é utilizada em algumas situações, como nos mostradores de alguns relógios, na escrita dos números dos séculos, na numeração de capítulos de livros e de leis, na designação de reis e papas de mesmo nome, etc.
O sistema de numeração decimal
Muitas civilizações antigas criaram seus próprios sistemas de numeração. Um deles, criado na Índia, deu origem ao sistema de numeração que hoje usamos. Depois de aperfeiçoado, esse sistema apresentou características que o tornaram mais prático que os outros. Vamos resumir essas características:
- As quantidades de 1 a 9 têm símbolos diferentes para representá-las.
- O sistema é decimal ou de base 10, ou seja, agrupamos de 10 em 10.
- Possui um símbolo (o zero) para representar no número a ausência de unidades, dezenas, centenas, etc.
- Com somente dez símbolos (os algarismos) é possível registrar todos os números, pois o mesmo algarismo assume valor diferente de acordo com sua posição na escrita do número.
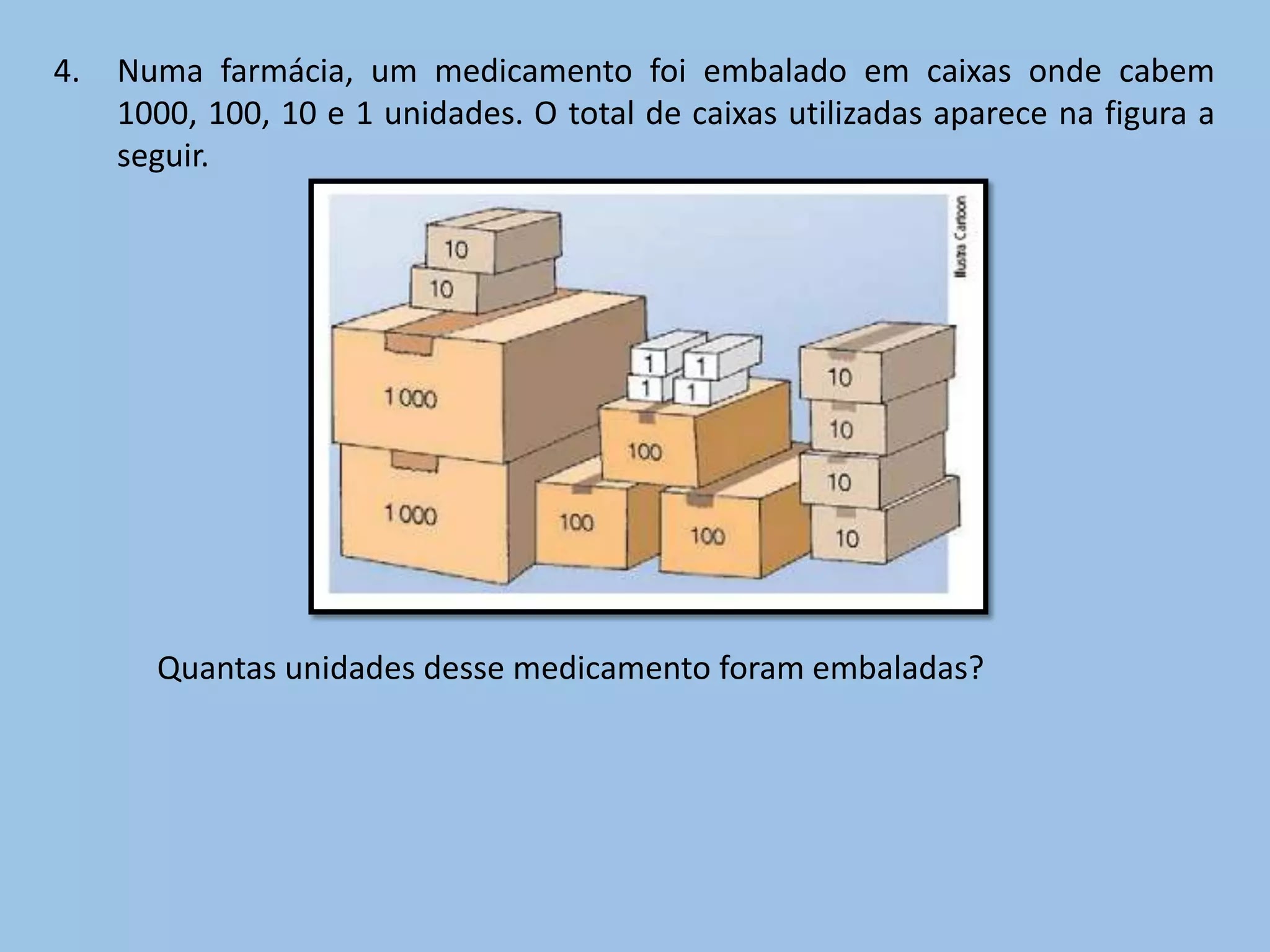
4. Numa farmácia, um medicamento foi embalado em caixas onde cabem 1000, 100, 10 e 1 unidades. O total de caixas utilizadas aparece na figura a seguir. Quantas unidades desse medicamento foram embaladas?
5. Numa gincana ficou acertado que:
- Cada ponto valeria um cartão branco;
- Quando uma equipe fizesse 10 pontos, trocaria os cartões brancos por um cartão azul;
- Quando uma equipe juntasse 10 cartões azuis, trocaria por 1 cartão vermelho.
Veja o resultado no final das provas:
a) Quantos pontos fez cada equipe?
b) Qual é a equipe vencedora?
c) Qual equipe fez menos pontos?
d) O que aconteceria com a equipe B se tivesse conseguido mais 2 cartões brancos?
Leitura e escrita de números no sistema de numeração decimal
Cheques, recibos, notícias ... É preciso saber ler e escrever os números corretamente para não ter dificuldades na vida prática!
Segundo dados do IBGE (Instituto Brasileiro de Geografia e Estatística), em certo momento do ano de 2010 a população brasileira era de 190732694 habitantes.
Lê-se: cento e noventa milhões, setecentos e trinta e dois mil, seiscentos e noventa e quatro habitantes. Esse número tem 9 algarismos. Partindo da direita para a esquerda, cada algarismo corresponde a uma ordem. Note que também separamos os algarismos da direita para a esquerda em grupos de três ordens.
Cada grupo desses forma uma classe.
Assim, temos: À esquerda da classe dos milhões vem a classe dos bilhões, depois dela, a classe dos trilhões, dos quatrilhões, e assim por diante.
PESQUISA
Nas manchetes e reportagens de jornais e revistas é comum encontrarmos números. Procurem, recortem e colem no caderno:
a) Um número que tenha 5 ordens.
b) Um número que tenha o algarismo 4 na ordem das centenas.
c) Um número que tenha o algarismo 2 na ordem das unidades de milhão.
d) Um número que tenha o zero na ordem das unidades de milhar.
e) Um número que tenha a classe dos bilhões.
f) Escreva por extenso cada um dos números encontrados.
Professor Rubens www.rubensdiasjr.blogspot.com.br























Nenhum comentário:
Postar um comentário