Atividades de Matemática
Funções Exponenciais: Aplicação e Características
Na disciplina de Matemática da 1º ano, exploramos o conceito de funções exponenciais e sua aplicação em diversas áreas, como Biologia, Química e Saúde. O objetivo principal é identificar e compreender essas funções, além de analisar seu comportamento através de representações gráficas.
Identificação e Compreensão de Funções Exponenciais
Ao longo da aula, buscamos entender o que caracteriza uma função exponencial. Discutimos como reconhecer se uma função é crescente ou decrescente com base em sua representação gráfica e seu sinal. Além disso, destacamos a importância de identificar padrões de crescimento ou decrescimento em dados numéricos apresentados na forma de potências.
MATEMÁTICA 1o ANO Gráfico da função exponencial
Objetivos da aula: - Identificar uma Função Exponencial - Reconhecer o crescimento ou o decrescimento de uma Função Exponencial por meio de seu sinal e/ou representação gráfica.
ESTUDANTE, PENSE... Você sabe identificar uma função exponencial? Você sabe reconhecer quando uma função é crescente ou decrescente?
Cissiparidade, divisão binária ou bipartição é um tipo de reprodução assexuada realizada por seres, como as bactérias, por exemplo. Uma bactéria se divide, formando duas idênticas. Função Exponencial na Biologia
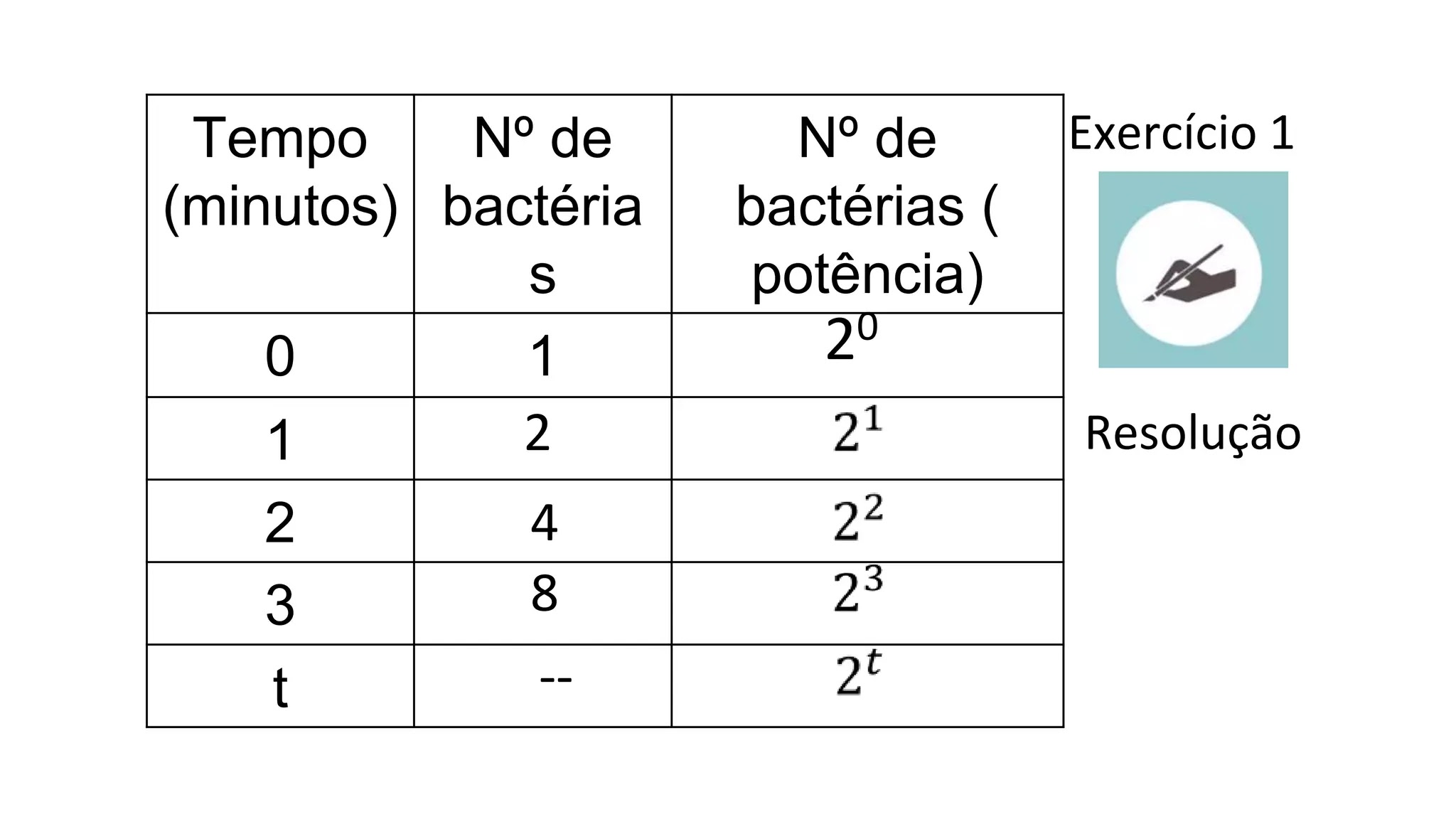
Exercício 1 Considere, inicialmente, uma bactéria que se reproduz, assexuadamente, por meio da cissiparidade e gera indivíduos iguais a cada minuto. a) Represente no quadro a seguir o número de bactérias a cada minuto e em forma de potência:
Exercício 1 Tempo (minutos) Nº de bactéria s Nº de bactérias ( potência) 0 1 1 2 3 t 2 4 8 -- Resolução 20
Exercício 1 b) O número de bactérias dobra a cada minuto. Escreva uma função que relacione o número de bactérias n em função do tempo t e represente no gráfico.
Exercício 1 Resolução
A técnica utilizada para diagnosticar doenças em um indivíduo é denominada cintilografia, que consiste em injetar um isótopo radioativo, obtendo, dessa forma, a imagem de determinado órgão. Um radioisótopo utilizado para diagnosticar problemas com a glândula tireóidea é o iodo-123. Função Exponencial na Química e na Saúde
O iodo-123 é conveniente nessa técnica, pois a duração do efeito no organismo está relacionada à sua meia vida que é de 13 horas, de modo que a cada intervalo de 13 horas, a quantidade de iodo- 123 no organismo equivale a 50% da quantidade existente no início desse intervalo, isto é, metade da sua quantidade inicial se desintegra. Fonte: Medicina nuclear. Disponível em http://grupomnd.com.br/noticia/o-que- e-a-cintilografia-da-tireoide/. Acesso em 25 de junho de 2020.
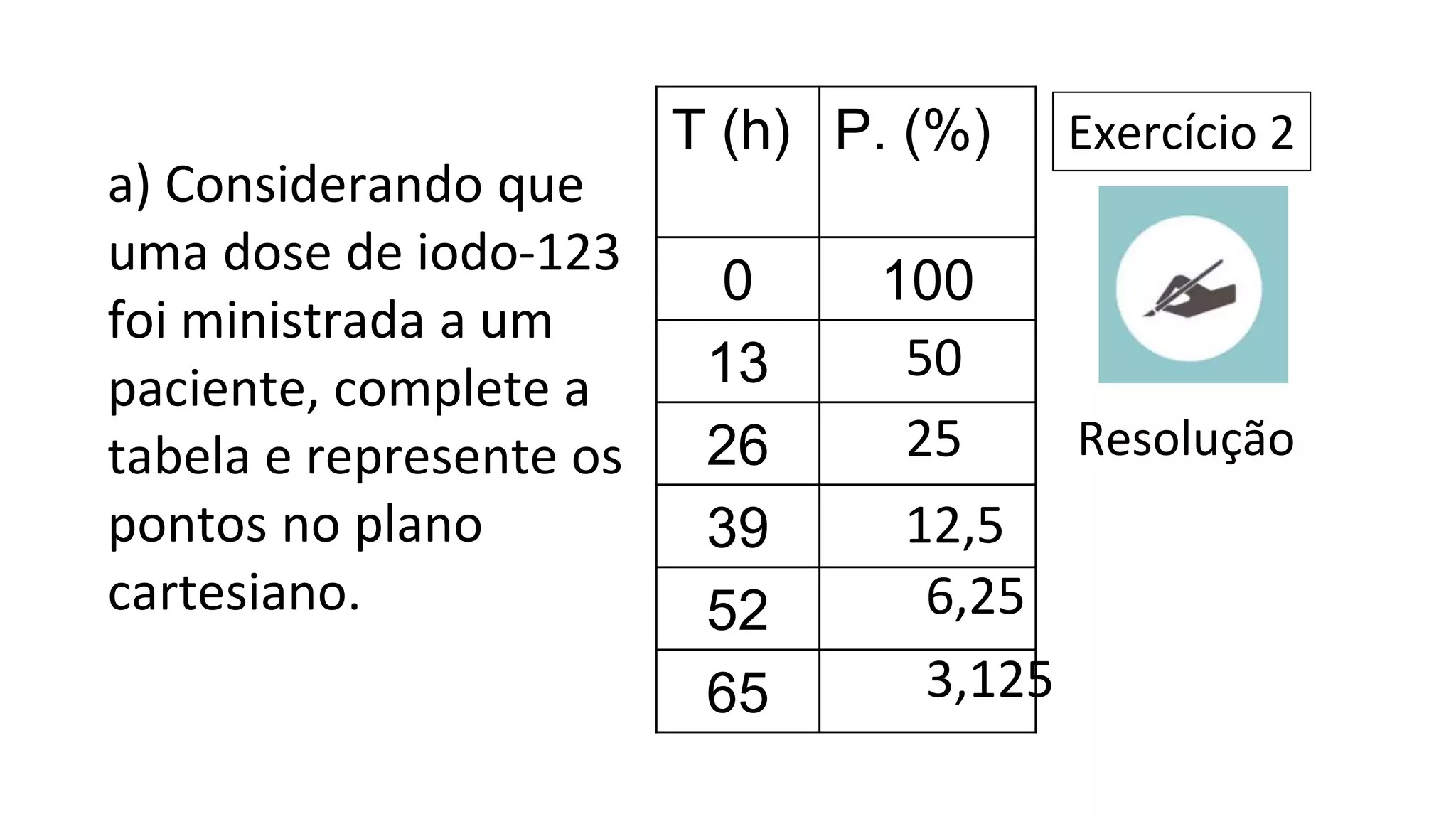
a) Considerando que uma dose de iodo-123 foi ministrada a um paciente, complete a tabela e represente os pontos no plano cartesiano. Exercício 2 T (h) P. (%) 0 100 13 26 39 52 65 50
a) Considerando que uma dose de iodo-123 foi ministrada a um paciente, complete a tabela e represente os pontos no plano cartesiano. Exercício 2 T (h) P. (%) 0 100 13 26 39 52 65 50 25 12,5 6,25 3,125 Resolução
Exercício 2 T (h) P. (%) 0 100 13 50 26 25 39 12,5 52 6,25 65 3,125 h % Resolução 0 100 50 10 20 30 50 60 40 40 30 20 10 70 80 60 70 80 90 Registre no caderno!
Características do gráfico da função exponencial • A curva da função f(x) = ax passa pelo ponto (0, 1) • O seu domínio é o conjunto dos reais D = R • O seu conjunto imagem é Im = R+ * • A função é crescente para a base a maior que 1 (a > 1)
Características do gráfico da função exponencial • O seu domínio é o conjunto dos reais D = R • O seu conjunto imagem é Im = R+ * • A função é decrescente para a base a maior que 0 e menor que 1 (0 < a < 1)
O que vimos: - Gráfico da função exponencial f(x) = ax - Características da função exponencial. - Aplicação da função exponencial em outras áreas.
Referências: DANTE, Luiz Roberto. Matemática: contexto & aplicações: ensino médio – vol 1 – 3. ed. – São Paulo: Ática, 2016. XAVIER, Cláudio & BARRETO, Benigno. Matemática: participação e contexto: ensino médio – volume único – São Paulo: FTD, 2008.

















Nenhum comentário:
Postar um comentário