GEOMETRIA ESPACIAL DE POSIÇÃO SLIDES.

Atividades de Matemática

• IDENTIDADE DE EULER - DEMONSTRAÇÃO.
• INTRODUÇÃO AO ESTUDO DOS POLIEDROS.
• QUESTÕES MATEMÁTICA CONCURSO PDF.

Geometria espacial de posição

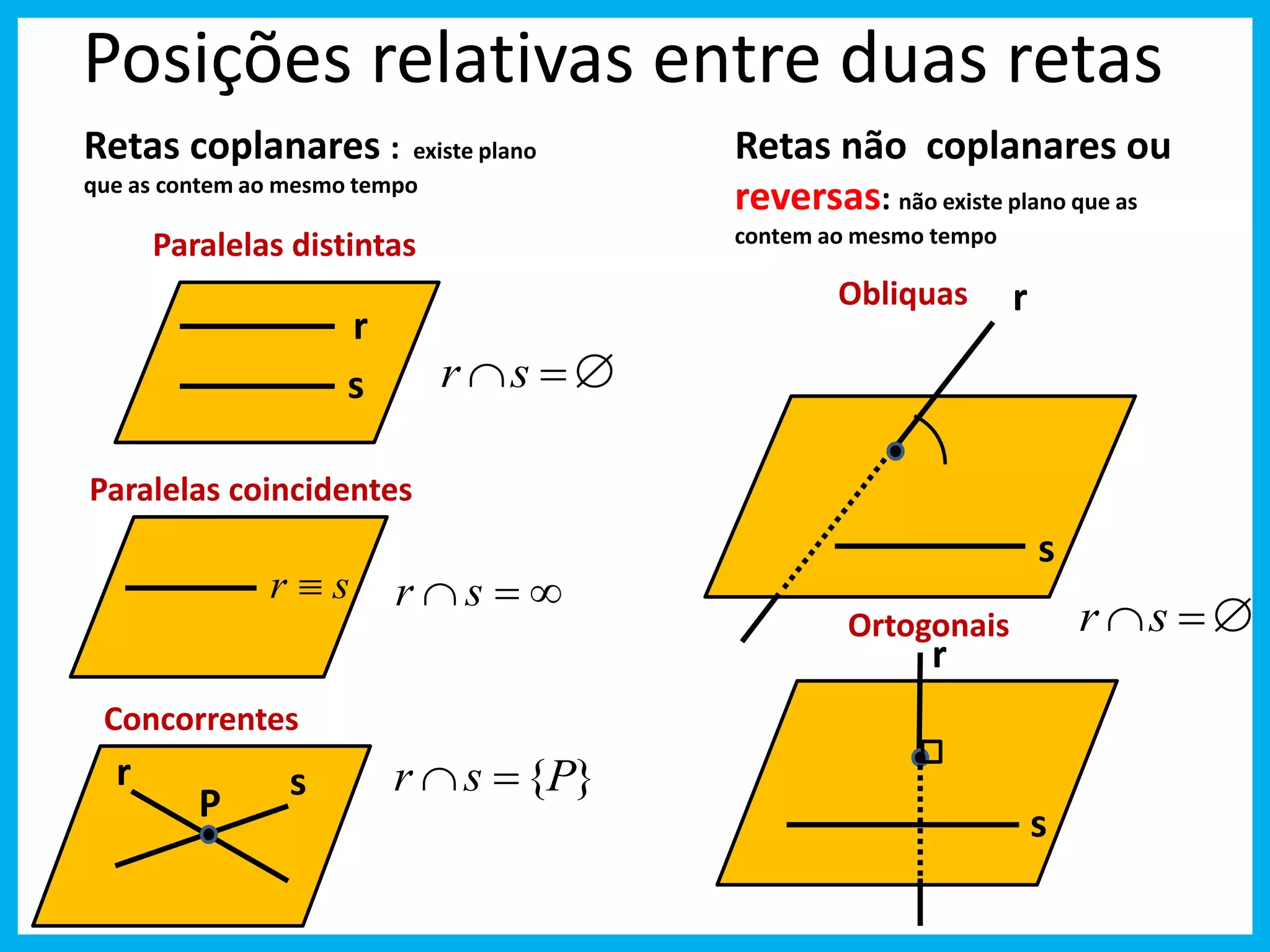
Posições relativas entre duas retas Retas não coplanares ou reversas: não existe plano que as contem ao mesmo tempo Paralelas distintas r s rs  Paralelas coincidentes r  s r s   Concorrentes r s rs {P} P Obliquas r s Ortogonais r s rs  Retas coplanares : existe plano que as contem ao mesmo tempo

 

Geometria espacial de posição Postulados

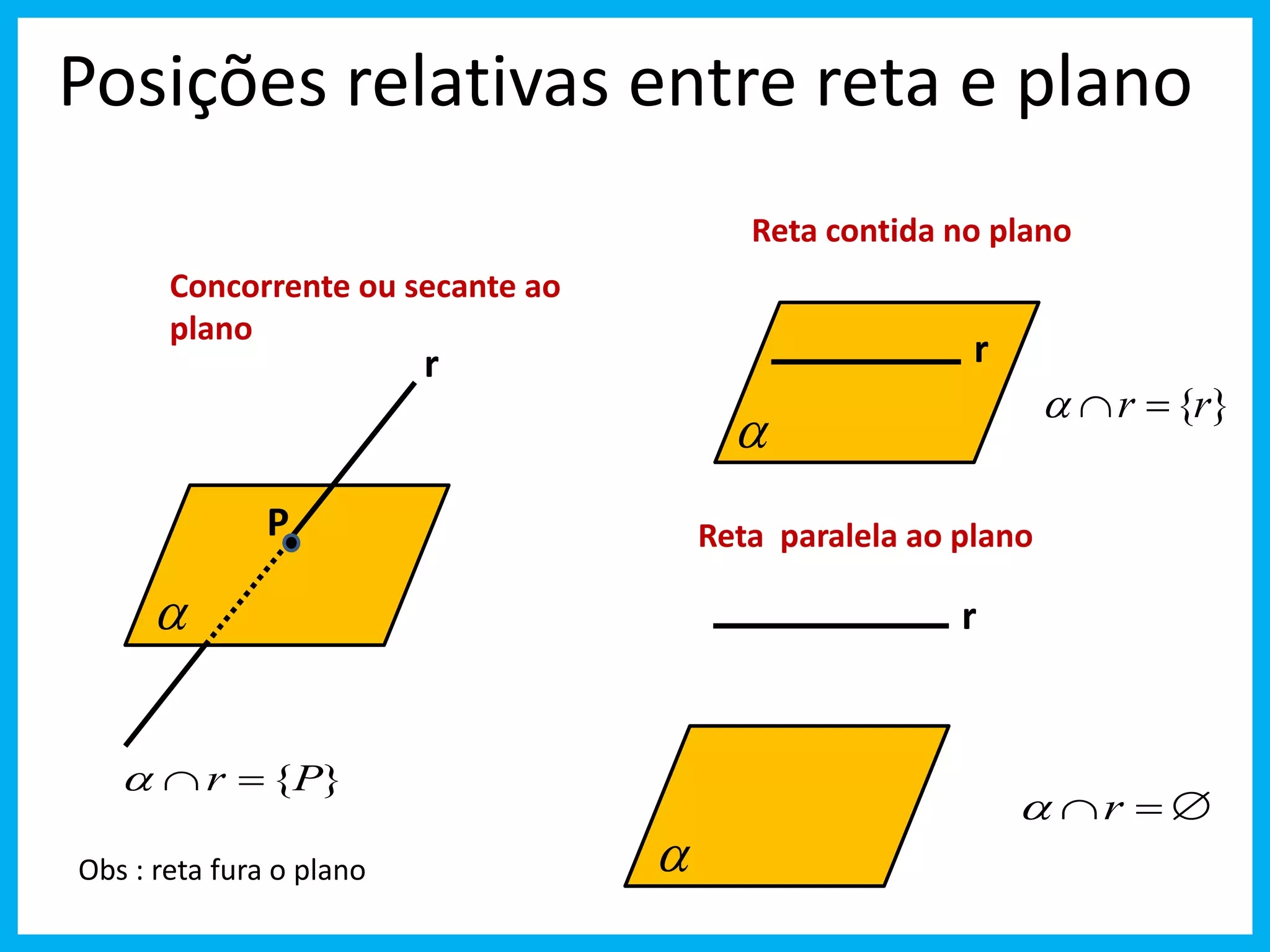
Posições relativas entre reta e plano Reta contida no plano Concorrente ou secante ao plano r r P   r {P}   r {r} Reta paralela ao plano r   r  Obs : reta fura o plano

Observações : Reta perpendicular ou ortogonal ao plano r  Reta paralela ao plano r 

Posições relativas entre dois planos   Concorrentes Paralelas Coincidentes         r   {r}

Geometria Espacial 

Poliedros Prof: ELIZEU - A superfície de um poliedro é formada por polígonos, chamados FACES do poliedro; - Os lados dos polígonos são chamados ARESTAS do poliedro; - Os vértices dos polígonos são os VÉRTICES do poliedro.

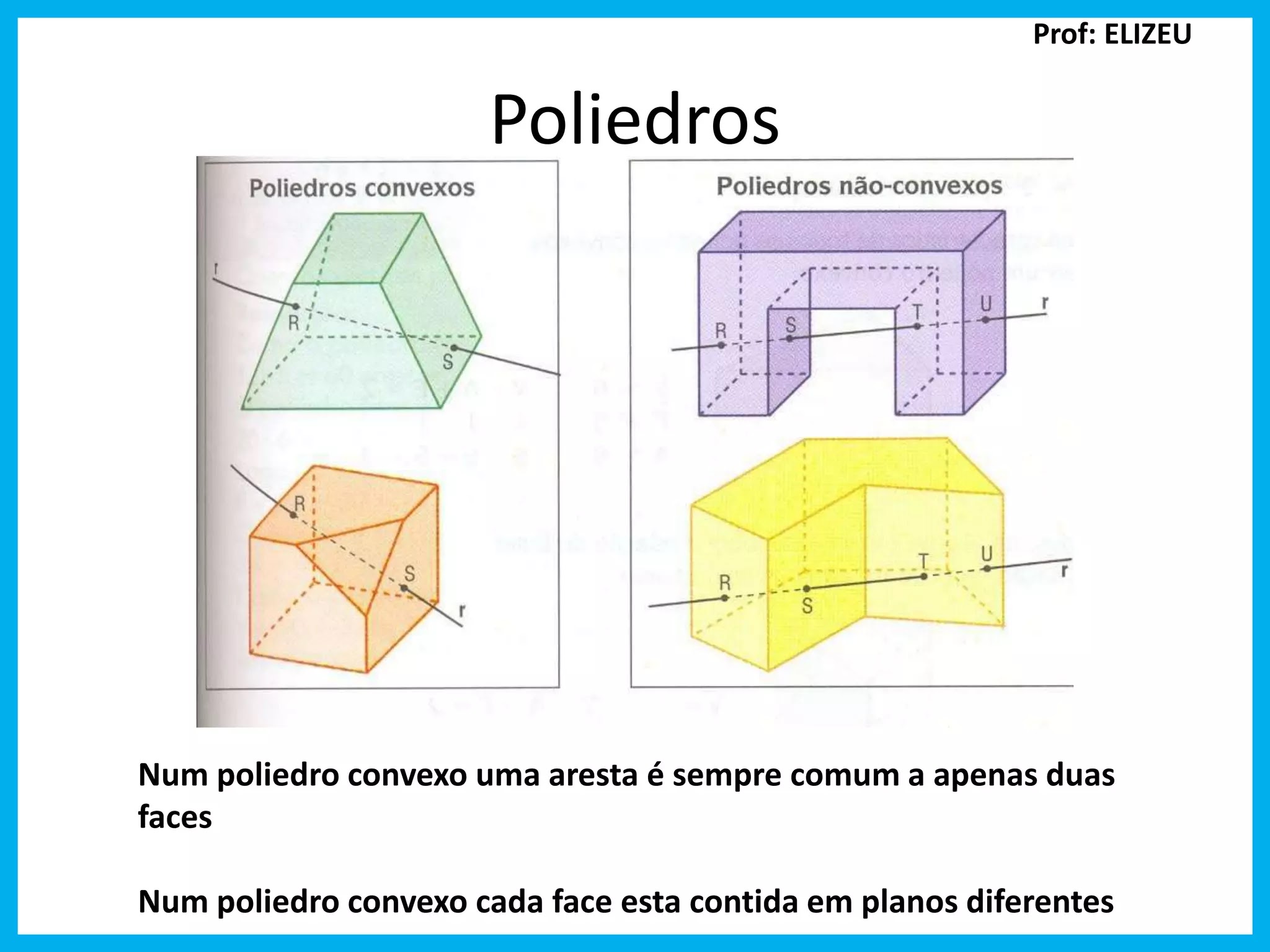
Poliedros Prof: ELIZEU Num poliedro convexo uma aresta é sempre comum a apenas duas faces Num poliedro convexo cada face esta contida em planos diferentes

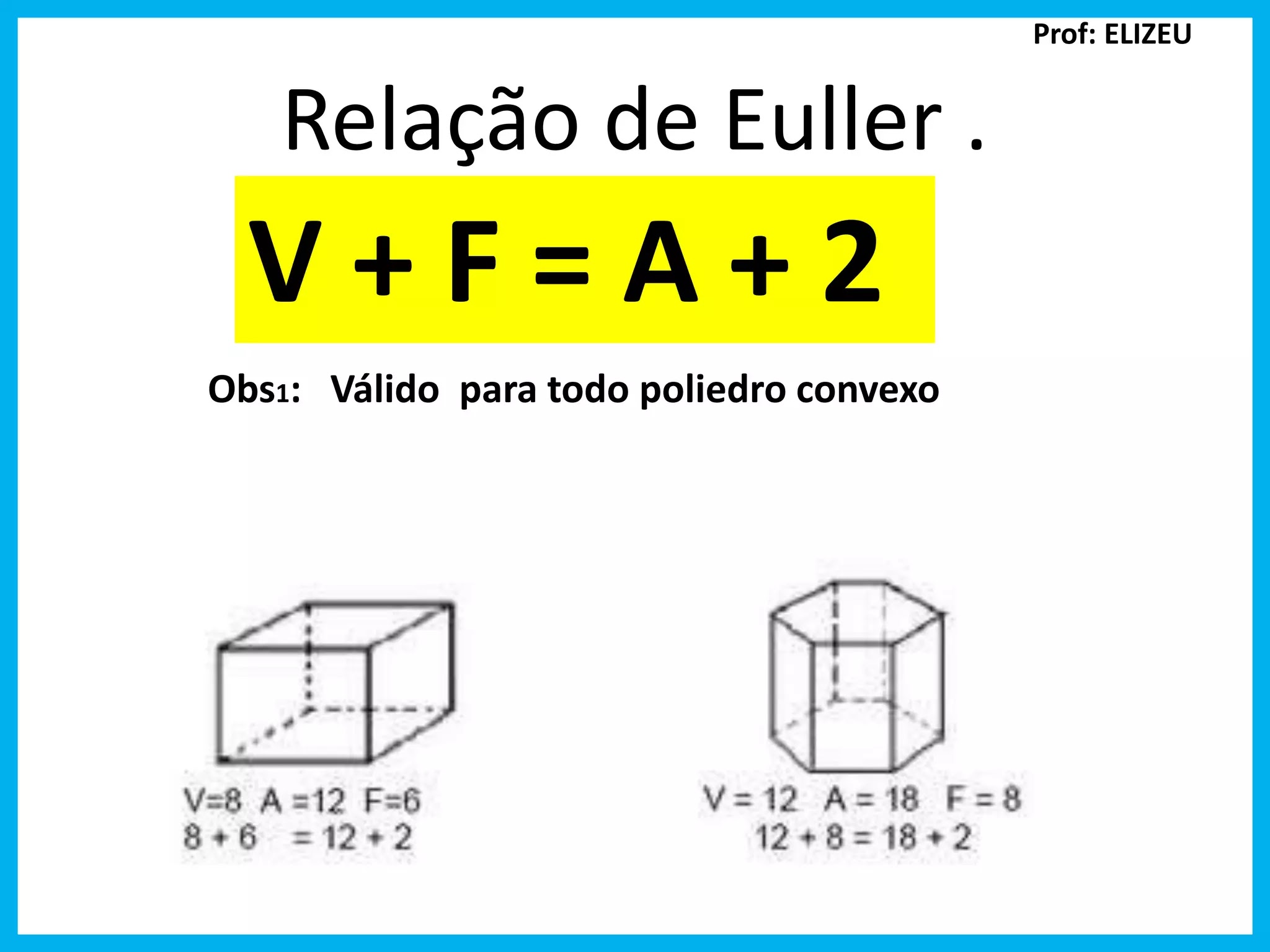
Relação de Euller . V + F = A + 2 Obs1: Válido para todo poliedro convexo Prof: ELIZEU

Prof: ELIZEU Ex1: Um poliedro convexo possui 12 faces e 8 vértices. Determine o número de arestas desse poliedro. Ex2: Um poliedro convexo possui exatamente 4 faces pentagonais e 6 faces triangulares. Determine o número de vértices desse sólido.

Poliedros de Platão Existem apenas cinco poliedros de Platão: - Tetraedro; - Hexaedro; -Octaedro; -Dodecaedro; -Icosaedro. Prof: ELIZEU Obs2: Se um poliedro convexo possui todas as faces formadas por polígonos regulares e congruentes, então ele é chamado de POLIEDRO REGULAR.