RAZÕES TRIGONOMÉTRICAS NO TRIÂNGULO RETÂNGULO
ATIVIDADES MATEMATICA
📕 RAZÕES TRIGONOMÉTRICAS EXERCÍCIOS PDF 📚
Razões trigonométricas no triângulo retângulo
1. MATEMÁTICA PRIMEIRA SÉRIE ENSINO MÉDIO Professora: SANDRA DI FLORA
2. RAZÕES TRIGONOMÉTRICAS NO TRIÂNGULO RETÂNGULO
3. A palavra Trigonometria tem origem grega: TRI (três), GONO (ângulo) e METRIEN (medida). Etimologicamente, significa medida de triângulos . Trata-se, assim, do estudo das relações entre os lados e os ângulos de um triângulo . Encontramos aplicações na mecânica, eletricidade, acústica, música, astronomia, engenharia, medicina, enfim, em muitos outros campos da atividade humana.
4. SENO, COSSENO e TANGENTE de um ângulo agudo (B) num triângulo retângulo sen B = cateto oposto ao ângulo B hipotenusa cos B = cateto adjacente ao ângulo B hipotenusa tan B = cateto oposto ao ângulo B cateto adjacente ao ângulo B = = = B + C = 90 o Cateto oposto Cateto adjacente hipotenusa A C B ( b) ( a) ( c)
5. SECANTE, COSSECANTE e COTANGENTE de um ângulo agudo Secante é a razão inversa do Cosseno Cossecante é a razão inversa do Seno Cotangente é a razão inversa do Tangente = = =
6. A razão de um ângulo agudo num triângulo retângulo é igual à co-razão do outro ângulo agudo desse triângulo (e vice-versa) ( + β = 90 ) PROPRIEDADE DOS ÂNGULOS COMPLEMENTARES
7. Exercícios iniciais








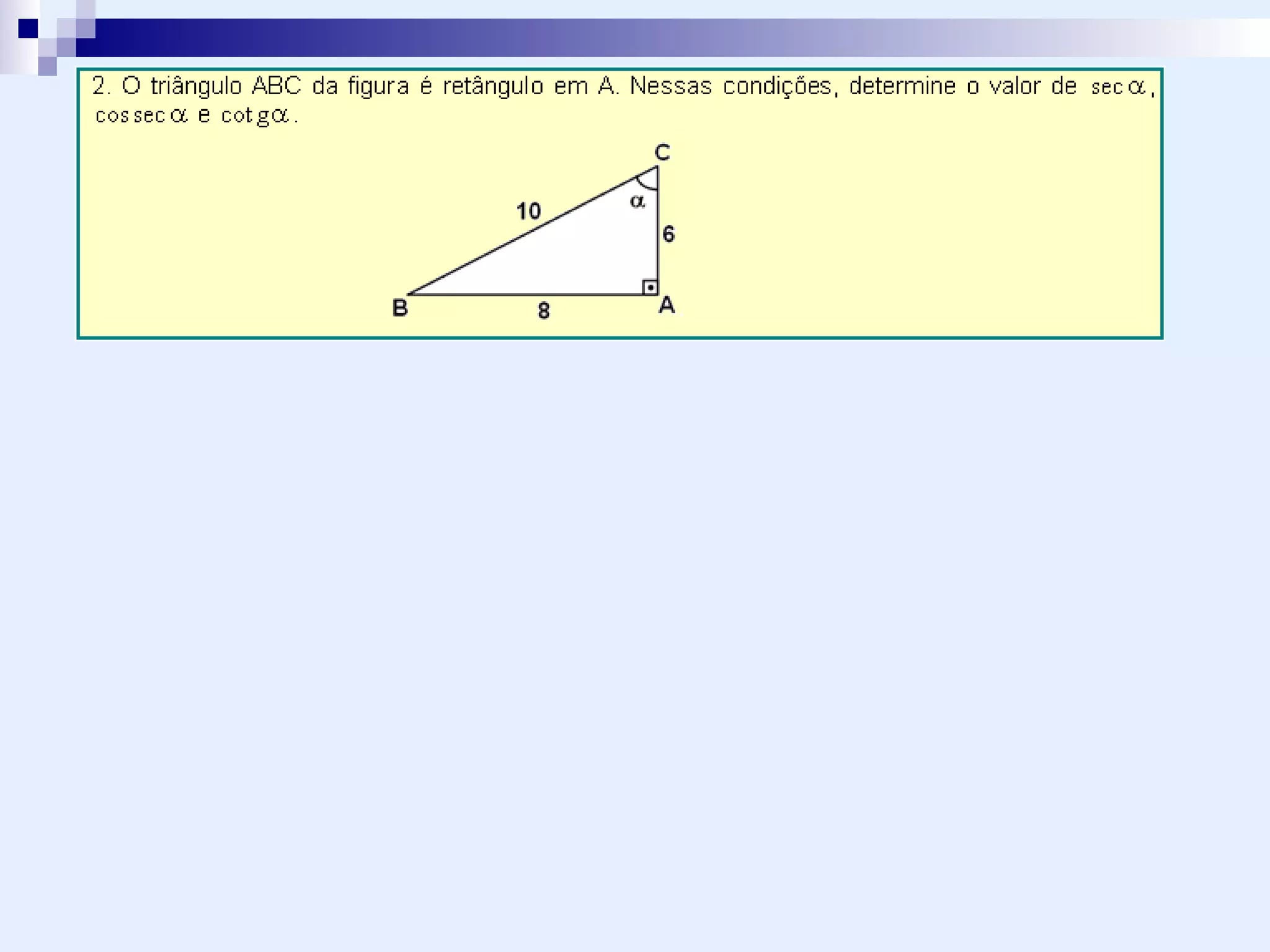
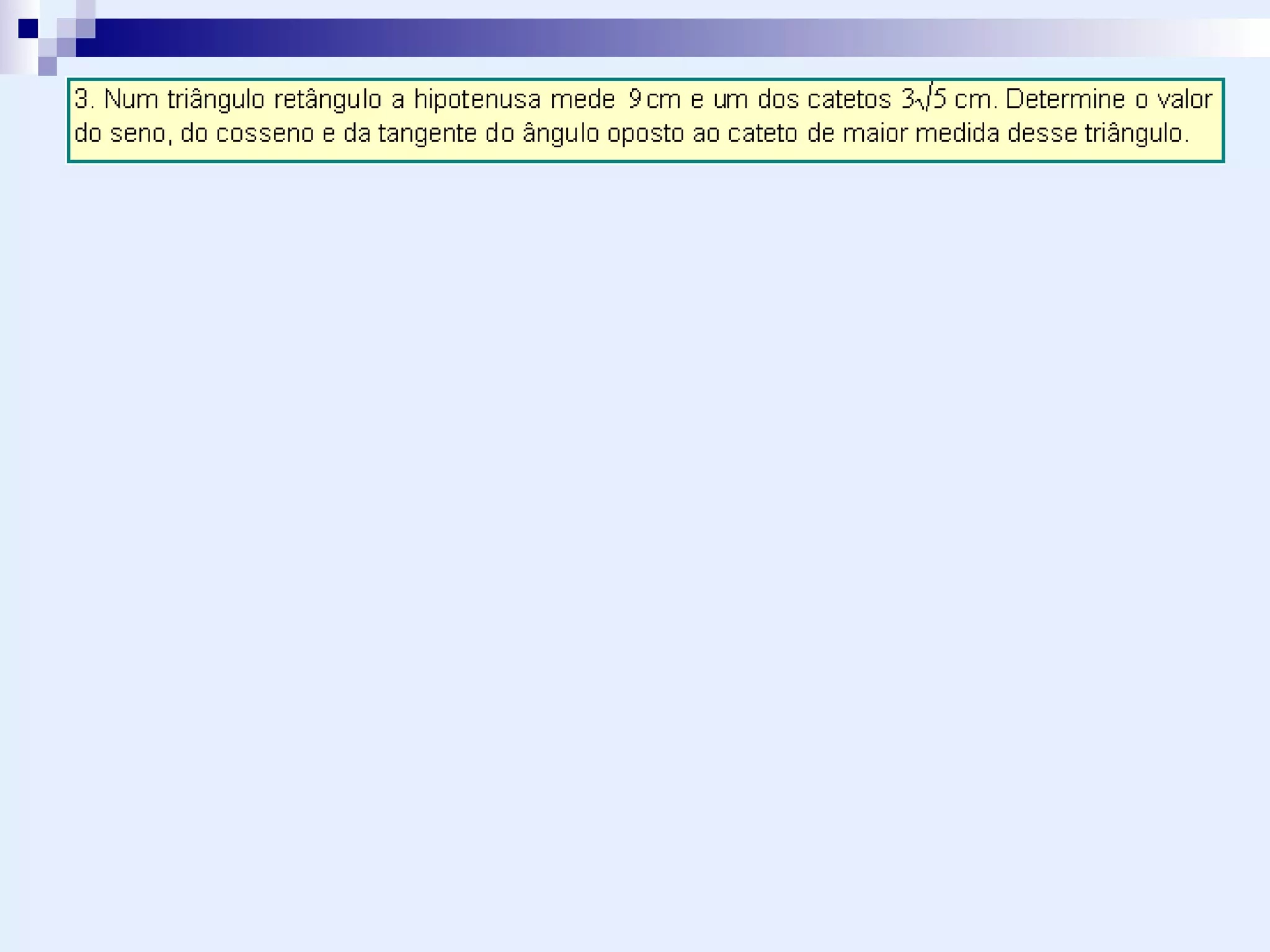


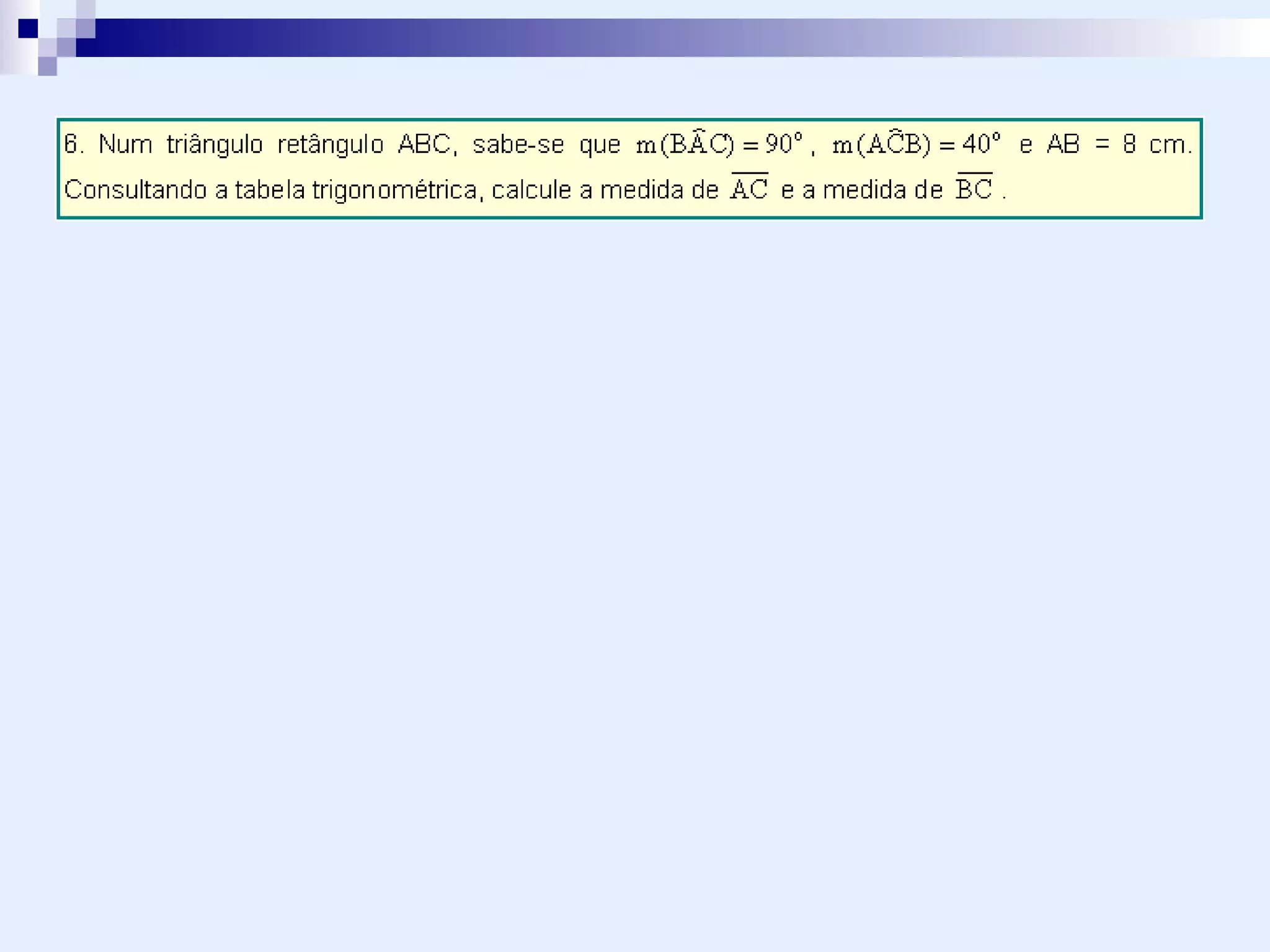



Nenhum comentário:
Postar um comentário