Exercícios de Matemática
- LISTA DE EXERCÍCIOS 8o ANO ÂNGULOS.
- PROBLEMAS PARA O 7° ANO / 8° ANO [COM GABARITO].
- 1000 QUESTÕES DE PORTUGUÊS PDF COM GABARITO.
Programa de Recuperação Paralela Prova de Matemática
📕 PROVA DE RECUPERAÇÃO 8 ANO 📚
8 ano matemática
1. COLÉGIO NOSSA SENHORA DA PIEDADE Programa de Recuperação Paralela 2ª Etapa – 2012 Disciplina: Matemática Professor (a): Rosângela Ano: 8º Turma: 8.1 e 8.2 Caro aluno, você está recebendo o conteúdo de recuperação. Faça a lista de exercícios com atenção, ela norteará os seus estudos. Utilize o livro didático adotado pela escola como fonte de estudo. Se necessário, procure outras fontes como apoio (livros didáticos, exercícios além dos propostos, etc.). Considere a recuperação como uma nova oportunidade de aprendizado. Leve o seu trabalho a sério e com disciplina. Dessa forma, com certeza obterá sucesso. Qualquer dúvida procure o professor responsável pela disciplina. Conteúdo Recursos para Estudo / Atividades Operações com medidas de ângulos Retas paralelas cortadas por transversal Semelhança de triângulos Triângulos Triângulo retângulo Altura, Bissetriz , Mediana e Mediatriz Conjuntos N, Z, Q, I, R Propriedades de potências de mesma base Operações com potências de mesma base Raiz quadrada (exata, decimal e fração) Valor numérico Monômios Polinômios: adição e subtração Livro Caderno Exercícios Avaliação diversificada Prova Intermediária Prova Trimestral
2. Rede de Educação Missionárias Servas do Espírito Santo Colégio Nossa Senhora da Piedade Av. Amaro Cavalcanti, 2591 – Encantado – Rio de Janeiro / RJ CEP: 20735042 Tel: 2594-5043 – Fax: 2269-3409 E-mail: cnsp@terra.com.br Home Page: www.cnsp.com.br ENSINO FUNDAMENTAL II Área de Conhecimento: Matemática e suas tecnologias Disciplina: Matemática Data : ____________/____________/2012 Etapa: 2ª Professora: Rosângela BLOCO DE ATIVIDADES / EXERCÍCIOS PROPOSTOS 1) A representação decimal do número √27 é: (A) 4,8... (B) 5,1... (C) 5,8... (D) 6,2... 2) O valor numérico de 2 x³ - x² - 3x, para x = - 2, é: (A) – 10 (B) - 14 (C) - 6 (D) 18 Nome do (a) aluno (a): Ano: 8º Turma: Nº
3. 3) Nesta figura, as retas r e s são paralelas e t é uma transversal. ASSINALE a afirmação FALSA: (A) 1 = 8, pois são alternos internos. (B) 4 = 8, pois são correspondentes. (C) 1 = 7, pois são alternos internos. (D) 2 = 6, pois são correspondentes. 4) Classificando as alternativas em verdadeiras ou falsas, MARQUE a correta. I) A bissetriz, além de dividir o ângulo em dois ângulos congruentes, intercepta o lado oposto no seu ponto médio. II) Mediana é o segmento determinado por um vértice e pelo ponto médio do lado oposto a este vértice. III) A altura é o segmento de reta que une um vértice ao lado oposto e é perpendicular a esse lado. (A) V, V, V (B) V, V, F (C) F, V, V (D) F, F, F 5) Dentre os números seguintes: a= 0,171717...; b= 0,313113111311113...; c= 0,424224222422224...; d= 0,897638976389763...; e = 3: (A) Nenhum é racional. (B) Todos são racionais. (C) Apenas e é racional. (D) Apenas a, d, e são racionais.
4. 6) Dois ângulos alternos internos formados por duas paralelas e uma transversal são: (A)adjacentes (B)congruentes (C) complementares (D) suplementares 7) Sobre as igualdades I. 0,757575... = II. 2,5333... = III. 1,444=...= É correto afirmar que: (A) Somente I é verdadeira. (B) Somente II é verdadeira. (C) Somente I e II são verdadeiras. (D) I, II e III são verdadeiras. 8) Os ângulos internos de um triângulo são: a , 5.a + 15° e 30°. Qual é a medida do ângulo a ? (A) 22° 30’ (B) 22° 45’ (C) 22° 50’ (D) 22° 55’
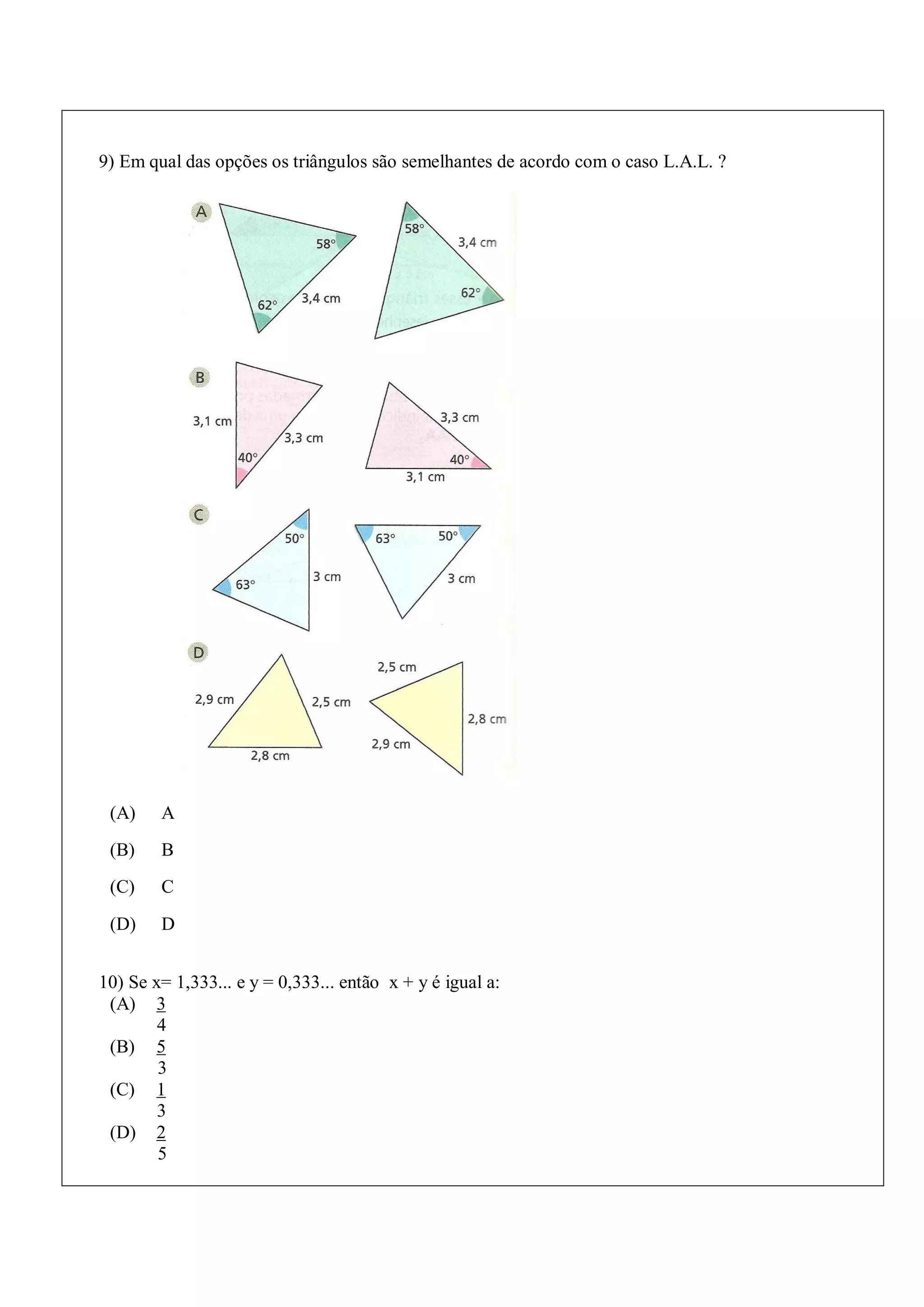
5. 9) Em qual das opções os triângulos são semelhantes de acordo com o caso L.A.L. ? (A) A (B) B (C) C (D) D 10) Se x= 1,333... e y = 0,333... então x + y é igual a: (A) 3 4 (B) 5 3 (C) 1 3 (D) 2 5
6. 11) Entre os números 5; -5; ; 5,5 e 5,555..., IDENTIFIQUE qual deles é: a) um número natural b) um número inteiro que não é natural c) um número racional inteiro e positivo d) racional, não inteiro, e sua representação decimal é finita e) racional com representação decimal infinita f) irracional 12)São dados os números 6; ; 6,6; 6,666...; ; -6 e 6,06660060006... IDENTIFIQUE os números que são: a) racionais b) irracionais 13) Dado o quadro abaixo, IDENTIFIQUE os números que pertencem ao conjunto dos números Inteiros. Resposta:___________________________________________________________________________
7. 14)Sabe-se que a= , e c= . Escrevendo esses números na forma decimal com aproximação até a 2ª casa decimal, CALCULE o valor de: a) + b) 5 - 15) Dada a expressão 6x² - 5x – 1, DETERMINE seu valor numérico quando x = -3? 16) Qual é o valor numérico da expressão + - 2a, quando a=4? 17) Dada a expressão algébrica 5y² - 18y – 8, qual é o seu valor numérico quando y = 4? 18) Considerando a expressão algébrica 2xy² + 3xy² + 5xy² - 7 xy², RESPONDA: a) A expressão é formada por quantos monômios? b) Todos monômios são semelhantes? c) Qual é a forma mais simples de escrever essa expressão? 19) Uma pequena fábrica de doces distribui seus produtos através de postos de vendas , , e , Separados entre si por distâncias que estão indicadas na figura. DETERMINE o monômio que representa a distância de F à . 20) SIMPLIFIQUE cada uma das expressões: a) x – ( -2x + 5x) + ( 7x – 4x) b) 10xy – [ -3xy + ( 9xy – 2xy) – xy]
8. 21) CALCULE: a) ( 3x² - 2x – 2) + ( x² + 1) + (x + 1)= b) (2y² - 5x + 1) – ( y² - 12 x + 7)= 22) CALCULE: a) (5x²) . (8x)= b) (-2a²bc) . ( 9ab³c)= c) ( mx²) . ( mx²)= d) ( 15 ) : ( - 5 )= e) ( 36 b ) : ( -9 a² c³) = f) = g) ( = h) = 23) Qual é a expressão que representa o perímetro dessa figura? x + 1 2 x + 1
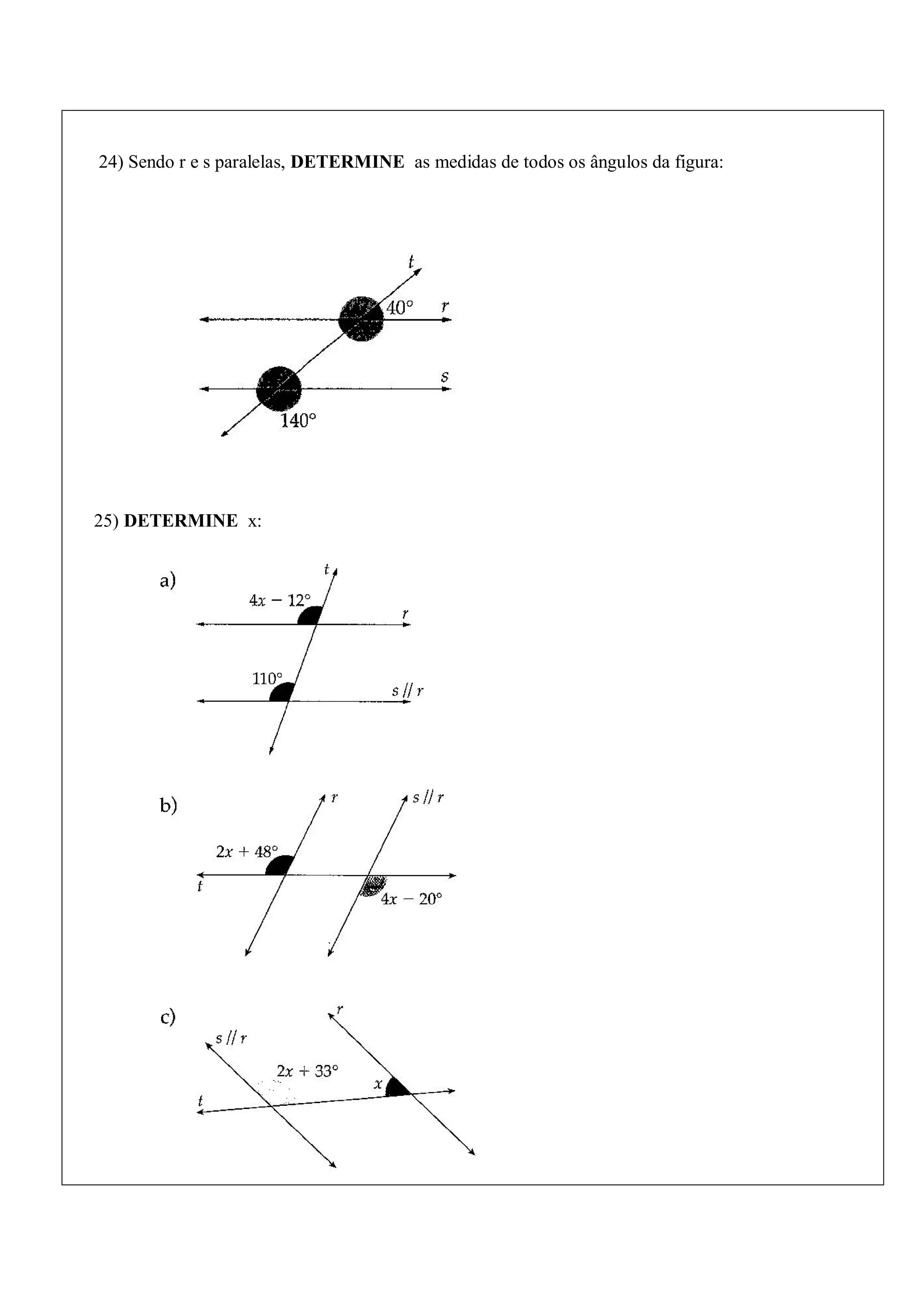
9. 24) Sendo r e s paralelas, DETERMINE as medidas de todos os ângulos da figura: 25) DETERMINE x:
10. 26) ENCONTRE o valor de a+b+c, sendo r//s: 27)No triângulo, AD é bissetriz. CALCULE x e y. 28)DETERMINE as medidas dos ângulos Â, B e C do triângulo.
11. 29)A hipotenusa de um triângulo retângulo mede 15m, um dos catetos mede 12m. Quanto mede o outro cateto? 30)CALCULE os ângulos indicados pelas letras:













Nenhum comentário:
Postar um comentário